Superposition Theorem
According to this theorem, if there ar variety of e.m.fs. acting at the same time in any linear bilateral network, then every e.m.f. acts severally of the others i.e. as if the opposite e.m.fs. didn't exist. the worth of current in any conductor is that the pure mathematics total of the currents because of every e.m.f. Similarly, voltage across any conductor is that the pure mathematics total of the voltages that every e.m.f would have created whereas acting separately.
In different words, current in or voltage across, any conductor of the network is obtained by superimposing the currents and voltages because of every e.m.f. within the network. it's necessary to stay in mind that this theorem is applicable solely to linear networks wherever current is linearly associated with voltage as per Ohm’s law.
Hence, this theorem is also expressed as follows : during a network of linear resistances containing quite one generator (or supply of e.m.f.), the present that flows at any purpose is that the total of all the currents which might flow at that time if every generator wherever thought-about individually and every one the opposite generators replaced for the nowadays by resistances adequate to their internal resistances.
Explanation
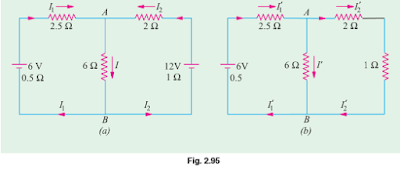
In Fig. 2.95 (a) I1, I2 and that i represent the values of currents that ar because of the coincident action of the 2 sources of e.m.f. within the network. In Fig. 2.95 (b) ar shown the present values which might are obtained if left-hand facet battery had acted alone.
Similarly, Fig. 2.96 represents conditions obtained once right-hand facet battery acts alone. By combining the present values of Fig. 2.95 (b) and a couple of.96 the particular values of Fig. 2.95 (a) are often obtained.
Obviously, I1 = I1' - I1'' , I2 = I2'' - I2´, I = I' + I''
Thanks by Rana...
According to this theorem, if there ar variety of e.m.fs. acting at the same time in any linear bilateral network, then every e.m.f. acts severally of the others i.e. as if the opposite e.m.fs. didn't exist. the worth of current in any conductor is that the pure mathematics total of the currents because of every e.m.f. Similarly, voltage across any conductor is that the pure mathematics total of the voltages that every e.m.f would have created whereas acting separately.
In different words, current in or voltage across, any conductor of the network is obtained by superimposing the currents and voltages because of every e.m.f. within the network. it's necessary to stay in mind that this theorem is applicable solely to linear networks wherever current is linearly associated with voltage as per Ohm’s law.
Hence, this theorem is also expressed as follows : during a network of linear resistances containing quite one generator (or supply of e.m.f.), the present that flows at any purpose is that the total of all the currents which might flow at that time if every generator wherever thought-about individually and every one the opposite generators replaced for the nowadays by resistances adequate to their internal resistances.
Explanation
In Fig. 2.95 (a) I1, I2 and that i represent the values of currents that ar because of the coincident action of the 2 sources of e.m.f. within the network. In Fig. 2.95 (b) ar shown the present values which might are obtained if left-hand facet battery had acted alone.
Similarly, Fig. 2.96 represents conditions obtained once right-hand facet battery acts alone. By combining the present values of Fig. 2.95 (b) and a couple of.96 the particular values of Fig. 2.95 (a) are often obtained.
Obviously, I1 = I1' - I1'' , I2 = I2'' - I2´, I = I' + I''
Thanks by Rana...
Superposition Theorem
 Reviewed by I will write articles or blogs containing 500 words for you.....
on
April 09, 2019
Rating:
Reviewed by I will write articles or blogs containing 500 words for you.....
on
April 09, 2019
Rating:
 Reviewed by I will write articles or blogs containing 500 words for you.....
on
April 09, 2019
Rating:
Reviewed by I will write articles or blogs containing 500 words for you.....
on
April 09, 2019
Rating:









No comments: