This theorem may be explicit either in terms of voltage sources or current sources or each.
(a) As Applicable to Voltage Sources
This Theorem could be a combination of Thevenin’s and Norton’s theorems. it's used for locating the common voltage across any network that contains variety of parallel voltage sources as shown in Fig. 2.221 (a). Then common voltage VAB that seems across the output terminals A and B is suffering from the voltage sources E1, E2 and E3. the worth of the voltage is given by
This voltage represents the Thevenin’s voltage Vth. The resistance Rth is found, as usual, by exchange every voltage supply by a brief circuit. If there's a load resistance RL across the terminals A and B, then load current IL is given by
IL = Vth/(Rth + RL)
If as shown in Fig. 2.222 (b), a branch doesn't contain any voltage supply, constant procedure is employed except that the worth of the voltage for that branch is equated to zero as illustrated in Example two.210.
Example 2.110.
Use Millman’s theorem, to find the common voltage across terminals A and B and the load current in the circuit of Fig. 2.222.
DC Network Theorems 159
Solution. As per Millman’s Theorem,
(b) As Applicable to Current Sources
This theorem is applicable to a mix of parallel voltage and current supplys that ar reduced to one final equivalent supply that is either a relentless current or a relentless voltage source.
This theorem is explicit as follows : Any variety of constant current supplys that ar directly connected in parallel is regenerate into one current supply whose current is that the algebraical add of the individual supply currents and whose total internal resistances equals the combined individual source resistances in parallel.
Example 2.111. Use Millman’s theorem, to find the voltage across and current through the load resistor RL in the circuit of Fig. 2.223 (a).
Solution. very first thing to try and do is to convert the given voltage sources into equivalent current sources. It ought to be unbroken in mind that the 2 batteries ar connected in wrong way. mistreatment supply conversion technique given in Art. 1.14 we tend to get the circuit of Fig. 2.223 (b).
The algebraic sum of the currents = 5 + 3 − 4 = 4 A. The combined resistance is = 12 || 4 || 6 = 2 Ω. The simplified circuit is shown in the current–source form in Fig. 2.224 (a) or voltage source form in Fig. 2.224 (b).
As seen from Fig. 2.224 (c).
IL = 8/(2 + 8) = 0.8 A ; VL = 8 × 0.8 = 64 V
Alternatively, VL = 8 × 8/(2 + 8) = 6.4 V
Following steps are necessary when using Millman’s Theorem :
1. convert all voltage sources into their equivalent current sources.
2. calculate the algebraic sum of the individual dual source currents.
Millman’s Theorem
 Reviewed by I will write articles or blogs containing 500 words for you.....
on
April 10, 2019
Rating:
Reviewed by I will write articles or blogs containing 500 words for you.....
on
April 10, 2019
Rating:
 Reviewed by I will write articles or blogs containing 500 words for you.....
on
April 10, 2019
Rating:
Reviewed by I will write articles or blogs containing 500 words for you.....
on
April 10, 2019
Rating:



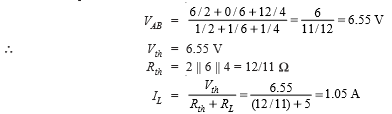








No comments: